How To Calculate Square Root Of Any Number | Best 4 Ways to Find Square Root
Calculation is always very important step in mathematics today we discussed about How To Calculate Square Root or how to find Square root of any number.
Table of Contents
Definition of Square Root
square root, in mathematics, a factor of a number that, when multiplied by itself, gives the original number. For example, both 3 and –3 are square roots of 9.
What is square root definition for kids?
The square root of a number is a value that can be multiplied by itself to give the original number. The square root of 9 is 3, because when 3 is multiplied by itself, you get 9.
Square Root Symbol
The square root symbol is usually denoted as ‘√’. It is called a radical symbol. To represent a number ‘x’ as a square root using this symbol can be written as:
‘ √x ‘
where x is the number. The number under the radical symbol is called the radicand. For example, the square root of 6 is also represented as radical of 6. Both represent the same value.
The operation of the square root of a number was already known in antiquity. The earliest clay tablet with the correct value of up to 5 decimal places of √2 = 1.41421 comes from Babylonia (1800 BC – 1600 BC). Many other documents show that square roots were also used by the ancient Egyptians, Indians, Greeks, and Chinese. However, the origin of the root symbol √ is still largely speculative.
- Many scholars believe that square roots originate from the letter “r” – the first letter of the Latin word radix meaning root.
- Another theory states that the square root symbol was taken from the Arabic letter ج that was placed in its original form of ﺟ in the word جذر – root (the Arabic language is written from right to left).
Who discovered √?
Regiomontanus is considered the inventor of the square root symbol. Prof Brown demonstrates how the algorithm starts by converting the input number N from base 10 to base 2.
Properties of Square root
Some of the important properties of the square root are as follows:
- If a number is a perfect square number, then there exists a perfect square root.
- If a number ends with an even number of zeros (0’s), then it can have a square root.
- The two square root values can be multiplied. For example, √3 can be multiplied by √2, then the result should be √6.
- When two same square roots are multiplied, then the result should be a radical number. It means that the result is a non-square root number. For instance, when √7 is multiplied by √7, the result obtained is 7.
- The square root of any negative numbers is not defined because the perfect square cannot be negative.
- If a number ends with 2, 3, 7 or 8 (in the unit digit), then the perfect square root does not exist.
- If a number ends with 1, 4, 5, 6 or 9 in the unit digit, then the number may have a perfect square root.
How do Find Square Root of Numbers?
If the number is a perfect square, such as 4, 9, 16, etc., then we can factorize the number by prime factorization method. If the number is an imperfect square, such as 2, 3, 5, etc., then we have to use a long division method to find the root.
Hence, the methods to find the square root of numbers are:
- Square Root by Prime Factorization
- Square Root by Repeated Subtraction Method
- Square Root by Long Division Method
- Square Root by Estimation Method
1. Square root By Prime Factorization
The square root of a perfect square number is easy to calculate using the prime factorization method. Let us solve some of the examples here:
| Number | Prime Factorization | Square Root |
| 16 | 2x2x2x2 | √16 = 2×2 = 4 |
| 144 | 2x2x2x2x3x3 | √144 = 2x2x3 = 12 |
| 169 | 13×13 | √169 = 13 |
| 256 | 256 = 2×2×2×2×2×2×2×2 | √256 = (2x2x2x2) = 16 |
| 576 | 576 = 2x2x2x2x2x2x3x3 | √576 = 2x2x2x3 = 24 |
2. Finding Square Roots by Repeated Subtraction Method
As per the repeated subtraction method, if a number is a perfect square, then we can determine its square root by:
- Repeatedly subtracting consecutive odd numbers from it
- Subtract till the difference is zero
- Number of times we subtract is the required square root
For example, let us find the square root of 25.
- 25 – 1 = 24
- 24 – 3 = 21
- 21 – 5 = 16
- 16 – 7 = 9
- 9 – 9 = 0
Since, the subtraction is done for 5 times, hence the square root of 25 is 5.
3. Finding Square Roots by Long Division Method
Step 1: Starting with the digit in the unit’s position, group the digits in pairs. Each pair and the
remaining digit (if any) is called a period. Starting from the right of the given number, place a bar over each pair of digits. If the number of digits is odd, the extreme left digit may not have a bar sign above it.
Step 2: Recognize the largest number whose square is equal to or slightly less than the first period. This number should be used as both a divisor and a quotient.
Step 3: Subtract the product of the divisor and the quotient from the first period and bring down the next period to the right of the remainder. This becomes the new dividend.
Step 4: The new divisor is created by multiplying the quotient by two and adding a suitable digit to it, which is also the quotient’s next digit. The product of the new divisor and this digit is equal to or less than the new dividend.
Step 5: Repeat steps 2, 3 and 4 till all the periods have been taken up. The final obtained quotient is the square root of the given number.
Find the square root of 65536.
Solution:
Step 1: Group the digits in pairs and place a bar over each pair of digits. The given number digits is odd, so the extreme left digit does not have a bar sign above it. That is, 6 55 36.
Step 2: The extreme left number here is 6. The largest number whose square is equal to or slightly less than 6 is 2. This number should be used as both a divisor and a quotient.
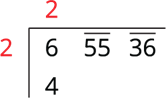
Step 3: Subtract the product of the divisor and the quotient from the first period and bring down the next period to the right of the remainder. That is 255. This becomes the new dividend.

Step 4: Find the new divisor, multiply the earlier quotient (2) by 2 (always) and write it, leaving a blank space next to it.
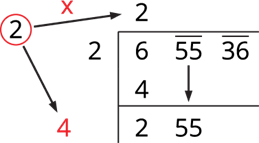
Step 5: The new divisor is 5, followed by a digit. We should choose this digit next to 4 such that the new quotient multiplied by the new divisor will be less than or equal to 255.
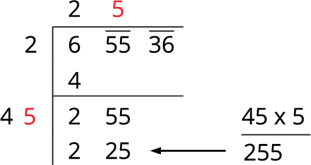
Now, subtract 225 from 255 and bring down the next period to the right of the remainder. That is 3036. This becomes the new dividend.
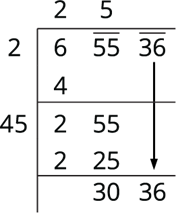
To find the new divisor, multiply the earlier quotient (25) by 2 (always) and write it, leaving a blank space next.

The new divisor is 50, followed by a digit. The required digit here has to be 6. We put 6 in the blank space and write 3036 below 3036 and subtract to get the remainder 0.

Therefore, √65536 = 256.
4. Square root by Estimation Method
This method is used as an approximation method, to find the square root by guessing the values.
For example, the square root of 4 is 2 and the square root of 9 is 3, thus, we can guess the square root of 5 will lie between 2 and 3.
But, we need to check the value of √5 is nearer to 2 or 3. Let us find the square of 2.2 and 2.8.
- 2.22 = 4.84
- 2.82 = 7.84
Since the square of 2.2 gives an approximate value of 5, thus we can estimate the square root of 5 is equal to 2.2 approximately.
Square Root Table (1 to 50)
Here is the list of the square root of numbers from 1 to 50.
| √n | Value | √n | Value | √n | Value |
| √1 | 1 | √18 | 4.2426 | √35 | 5.9161 |
| √2 | 1.4142 | √19 | 4.3589 | √36 | 6 |
| √3 | 1.7321 | √20 | 4.4721 | √37 | 6.0828 |
| √4 | 2 | √21 | 4.5826 | √38 | 6.1644 |
| √5 | 2.2361 | √22 | 4.6904 | √39 | 6.2450 |
| √6 | 2.4495 | √23 | 4.7958 | √40 | 6.3246 |
| √7 | 2.6458 | √24 | 4.8990 | √41 | 6.4031 |
| √8 | 2.8284 | √25 | 5 | √42 | 6.4807 |
| √9 | 3 | √26 | 5.0990 | √43 | 6.5574 |
| √10 | 3.1623 | √27 | 5.1962 | √44 | 6.6332 |
| √11 | 3.3166 | √28 | 5.2915 | √45 | 6.7082 |
| √12 | 3.4641 | √29 | 5.3852 | √46 | 6.7823 |
| √13 | 3.6056 | √30 | 5.4772 | √47 | 6.8557 |
| √14 | 3.7417 | √31 | 5.5678 | √48 | 6.9282 |
| √15 | 3.8730 | √32 | 5.6569 | √49 | 7 |
| √16 | 4 | √33 | 5.7446 | √50 | 7.0711 |
| √17 | 4.1231 | √34 | 5.8310 |
Square Root of Decimal
A decimal value will have a dot (.) such as 3.8, 5.2, 6.33, etc. For a whole number, we have understood how to derive the square root but let us see how to get the square root of a decimal.
| Example: Find the square root of 0.09.Let N2 = 0.09Taking root on both sides.N = ±√0.09As we know,0.3 x 0.3 = (0.3)2 = 0.09Therefore,N = ±√(0.3)2N = ±(0.3) |
Square Root of Negative Number
The square root of a negative number is not a real number but a complex number. It is because the square of any integer is a positive value. The square root of a negative number, say, -y, is: √(-y)= i√y, where ‘i’ is the square root of -1.
Square root of Complex Numbers
To find the square root of complex numbers is a little complicated. We can find the square root of a+ib using the below formula:
where a+ib is a complex number.
how to find square root of any number
How To Calculate Square Root Of Any Number | how to find square root | how to find square root of any number | Square Roots by Long Division Method
Square Root Calculator
How to find square root of decimal number
Solved Examples on Square Root Calculator
How To Calculate Square Root Of Any Number | how to find square root | how to find square root of any number | Square Roots by Long Division Method
Example 1:
Find the square root of 64 and verify it using the square root calculator.
Solution:
Using the Prime Factorization Method
64 = 2 × 2 × 2 × 2 × 2 × 2
64 = 22 × 22 × 22
64 = (2 × 2 × 2)2
64 = 82
√64 = 8
Therefore, 8 is the square root 64.
Example 2:
Find the square root of 25 and verify it using the square root calculator.
Solution:
Using the Prime Factorization Method
25 = 5 × 5
25 = 52
√25 = 5
Therefore, 5 is the square root 25.

